金属とプラスチックの強度の違い【材料力学的解説】

皆さんは金属とプラスチックの強度の違いを考えたことはありますか?
なんとなく金属は硬くて強度がある、プラスチックは壊れやすいというイメージがあるのではないでしょうか。
今回は数値的にどのくらい違いがあるのかを解説していきたいと思います。
代表材料
今回は板金で形を作った場合と、プラスチックで形を作った場合を比較するというケースを仮定してみます。
すると代表的な材料として、鉄系だとSPCCやSUS304などが採用されると思います。
アルミ系材料の板金の代表としては、A5052が最も一般的と思われるので、金属はSPCC,SUS304,A5052を代表として考えます。
一方でプラスチック材料としては、使用量の多い順に3つ選び、PMMA(アクリル),PP(ポリプロピレン),PC(ポリカーボネート)の3種類を代表に選びます。
各弾性係数は以下の表に示します。

圧縮強度

まずは圧縮強度について考えます。
材料を圧縮させたときの変位は、以下の式によって表されます。
$δ=\dfrac{FL}{EA}$・・・①
$δ$:圧縮量[$m$]
$F$:荷重[$N$]
$L$:材料の長さ[$m$]
$E$:材料のヤング率[$Pa$]
$A$:材料の断面積[$m^2$]
同じ形状・同じ荷重を与えた時、各材料でどのくらい変位に差が出るかを比較してみます。
SPCCの圧縮変位を1としたとき、他の材料は以下のようになります。
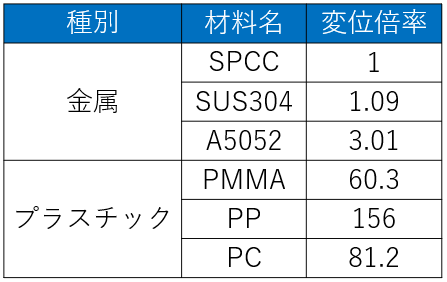
倍率の数字が大きいほど変位が大きく、強度が弱いということになります。
結果を見てみると、SPCCとSUS304はほぼ同じくらいであることが分かります。
しかしアルミの材料については3倍、プラスチック材料については約60~156倍も強度が劣ることが分かると思います。
ねじり強度
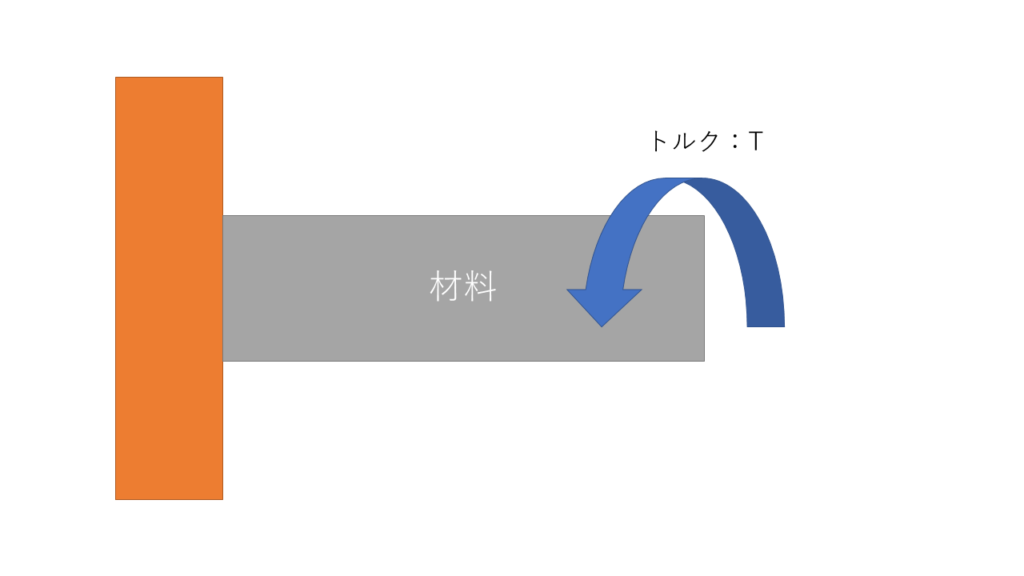
圧縮荷重と同じようにねじれ荷重も考えてみます。
ねじれ角を数式で表すと以下のようになります。
$φ=\dfrac{TL}{GI_p}$・・・②
$φ$:ねじれ角
$T$:トルク[$N・m$]
$L$:材料の長さ[$m$]
$G$:横弾性係数[$Pa$]
$I_p$:断面二次極モーメント[$m^4$]
材料に同じ大きさ・同じ荷重を与えた時のねじれ角を比較し、SPCCの結果を1としたときの倍率を以下の表に示します。
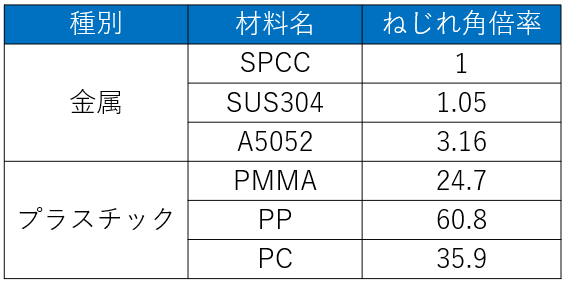
この結果を見ると、金属は圧縮荷重の場合とほぼ同じ値になっていますが、プラスチックの場合は約24~60倍ほど鉄より強度が劣ることになります。
曲げ強度
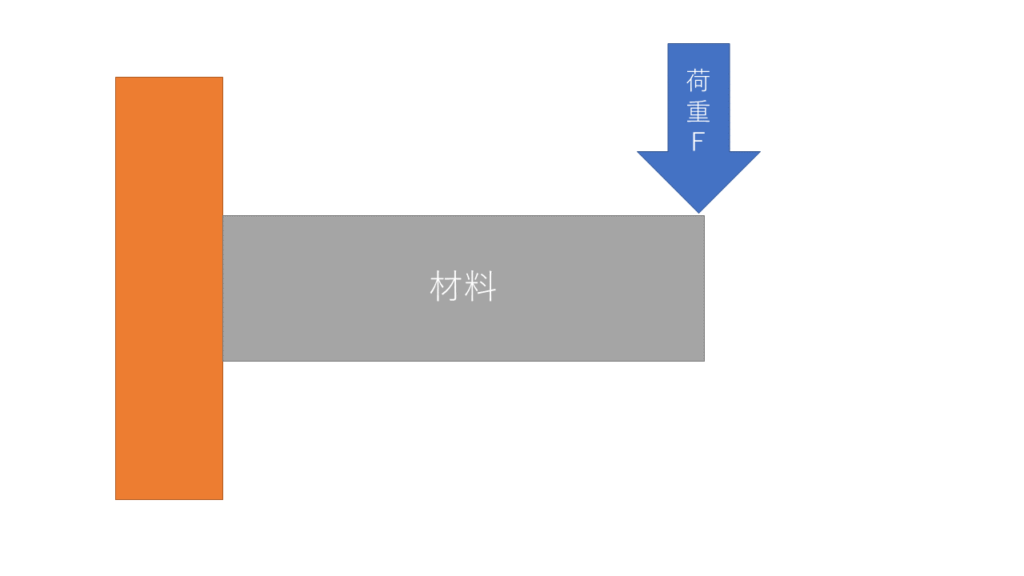
曲げ強度については、以下の式で表されます。
$δ=\dfrac{FL^3}{EI}$・・・③
$δ$:変位[$m$]
$F$:曲げ荷重[$N$]
$L$:材料の長さ[$m$]
$E$:ヤング率[$Pa$]
$I$:断面二次モーメント[$m^4$]
すると、圧縮強度と同様にヤング率によって強度が決まってしまいます。
つまり圧縮と同様の結果となります。
金属とプラスチックで同等の変形にするには?
金属とプラスチックで同じくらいの変形に抑えるには、どのような形状にすれば良いでしょうか?圧縮強度を例に考えてみます。
式①を金属の場合とプラスチックの場合でそれぞれ作り、同じ荷重で変位も等しいとすると、以下の式が成り立ちます。
$\dfrac{L_金}{L_{プラ}}\dfrac{A_{プラ}}{A_金}=\dfrac{E_金}{E_{プラ}}$・・・④
式④の右辺が結果の倍率に当たります。例としてPMMAの60.3倍を考えてみましょう。
このとき右辺の値は60.3なので、成り立つためには次の3パターンが考えられます。
- 長さは同じで、プラスチックの方が荷重を受ける面積が60.3倍大きい
- 面積が同じで、プラスチックの長さが60.3分の1
- プラスチックの方が短く、面積が大きく、面積比と長さ比の積が60.3
つまり弾性係数の比率分、面積を大きく、長さを短くすることによって、異なる材料でも同じ強度を実現できます。
まとめ
いかがだったでしょうか。
今回は金属とプラスチックの強度の違いについて解説してきました。
まとめると以下のようになります。
- 強度を比較するときは、弾性係数を考慮する
- 鉄と比較すると、プラスチックの圧縮強度は約60~156倍、ねじれ強度で考えると約24~60倍劣る
- 弾性係数の比率分、面積を大きく、長さを短くすることによって、異なる材料でも同じ強度を実現できる




















