梁の自重による影響とは?【材料力学的解説】

皆さんは梁の変形を考えるとき、自重の影響を考えていますでしょうか?
ビルや橋のような大きい建築物であれば、当然自重による影響は大きいと思いますが、プラスチックの小物入れのような場合であれば、軽いので影響は少ないように思えます。
今回は自重の影響について解説していきたいと思います。
重力の影響がない場合
まずは重力の影響がない場合を考えていきます。
片持ち梁と両端支持梁のそれぞれに荷重を与えた2つのパターンについて解説します。
支持方法はどちらも固定支持とします。

片持ち梁の場合
片持ち梁の場合、梁の最大変位は以下の式で表されます。
$δ_1=\dfrac{FL^3}{3EI}$
$δ_1$:梁の最大変位[$m$]
$F$:梁の先端にかかる荷重[$N$]
$L$:梁の長さ[$m$]
$E$:梁のヤング率[$Pa$]
$I$:梁の断面二次モーメント[$m^4$]
このように梁の変位は、荷重と長さの3乗に比例し、ヤング率と断面二次モーメントに反比例した値となります。
なお、最大変位の位置は梁の先端になります。
両端支持梁の場合
両端支持梁の場合、片持ち梁と数式が少し異なります。
$δ_2=\dfrac{FL^3}{192EI}$
$δ_2$:梁の最大変位[$m$]
$F$:梁の中央にかかる荷重[$N$]
$L$:梁の長さ[$m$]
$E$:梁のヤング率[$Pa$]
$I$:梁の断面二次モーメント[$m^4$]
片持ち梁と比較して、分母の係数が大きく変わっていることが分かると思います。
つまり最大変位で比べると、両端支持梁は片持ち梁の64倍変形しにくくなっていることになります。
重力の影響を加える場合
それではここから重力の影響を考慮した場合の変位を考えます。
前述の荷重を与えた場合の変位と重力による変位の2つを合計した値が最大変位となります。
片持ち梁の場合
片持ち梁の場合、最大変位を表す数式は以下のようになります。
$δ_3=\dfrac{FL^3}{3EI}+\dfrac{ρAgL^4}{8EI}$
$δ_3$:梁の最大変位[$m$]
$F$:梁の先端にかかる荷重[$N$]
$L$:梁の長さ[$m$]
$E$:梁のヤング率[$Pa$]
$I$:梁の断面二次モーメント[$m^4$]
$ρ$:材料の密度[$kg/m^3$]
$A$:梁の断面積[$m^2$]
$g$:重力加速度[$m/s^2$]
この場合、梁の長さ、断面二次モーメント、断面積、ヤング率が一定と考えると、梁の変位は荷重と密度のみによって決まることが分かります。
数式を少し変形してみると以下のようになります。
$δ_3=\dfrac{FL^3}{3EI}+\dfrac{ρAgL^4}{8EI}$
$=\dfrac{L^3}{3EI}$$(F+\dfrac{3ρAgL}{8})$
数式の( )内の前半部分が荷重による影響、後半が自重による影響を表しています。
つまり、$F$と$\dfrac{3ρAgL}{8}$の比較によってどちらの影響が大きいかが分かります。
両端支持梁の場合
両端支持梁の場合も同じように考えると、数式は以下のようになります。
$δ_4=\dfrac{FL^3}{192EI}+\dfrac{ρAgL^4}{384EI}$
$=\dfrac{L^3}{192EI}$$(F+\dfrac{ρAgL}{2})$
$δ_4$:梁の最大変位[$m$]
$F$:梁の先端にかかる荷重[$N$]
$L$:梁の長さ[$m$]
$E$:梁のヤング率[$Pa$]
$I$:梁の断面二次モーメント[$m^4$]
$ρ$:材料の密度[$kg/m^3$]
$A$:梁の断面積[$m^2$]
$g$:重力加速度[$m/s^2$]
片持ち梁のときと比較すると、( )内の重力の係数が3/8から1/2に変わっていることが分かると思います。
つまり、重力の影響は片持ち梁よりも両端支持梁の方が大きいことが分かります。
ただし、そもそも64倍変形しにくいので、絶対的な変形量としては両端支持梁の方が小さいことには注意が必要です。
材料による比較
それでは、具体的に材料を当てはめて考えてみましょう。
梁の形状は$10mm×10mm$角で、長さを$100mm$、先端にかかる荷重を$1N$とした場合、各材料での片持ち梁の最大変位は以下のようになります。
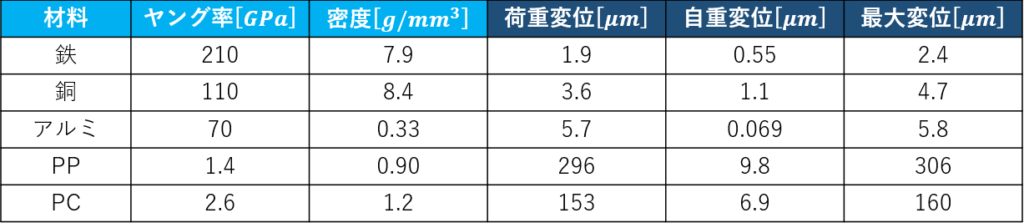
この結果より、鉄や銅のような密度の大きい材料の場合は、最大変位の内約20%ほど自重による影響を受けています。
一方でアルミやプラスチック類では、密度が小さいため、1~4%ほどしか影響がありません。
このように密度によって材料の自重の影響が大きくなることが分かると思います。
ただし、この計算は一例であり、梁形状と荷重によっても異なるため、注意が必要です。
両端支持梁の場合も結果は以下のようになります。
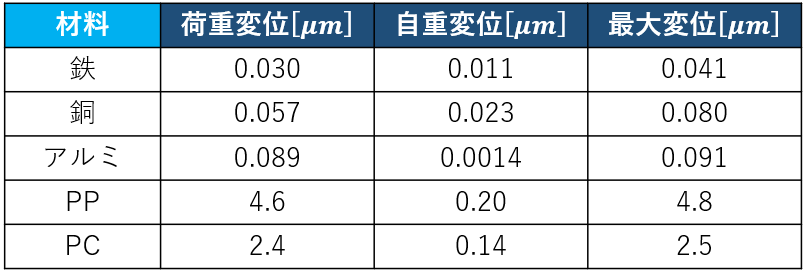
傾向は片持ち梁の場合とほぼ同じですが、鉄や銅の場合は自重の影響が27~29%ほど、アルミやプラスチック類は1.6~5.6%ほどで、若干ではありますが、自重の影響が増しています。
まとめ
いかがだったでしょうか。
今回は梁の変位と自重の影響について解説してきました。
まとめると以下のようになります。
- 梁の変位は荷重による変位と自重による変位の合計で表される
- 固定方法によって自重の影響力は変わってくる
- 密度が大きいほど自重による影響は大きくなる





















