皆さんは風の抵抗を考えたことはありますか?
向かい風の中で歩いていくときは、耐えられるだけの力が必要ですよね。
今回は風の抵抗を減らせる形状について解説していきます。
そもそも風の抵抗とは?
風の抵抗とは、風から受ける圧力と面積の積のことを指します。
数式で表すと以下のようになります。
$F=P・A$・・・②
$F$:風から受ける力[$N$]
$P$:風から受ける圧力[$Pa$]
$A$:風を受ける面積[$m^2$]
一方で風から受ける圧力はどのようになっているのでしょうか。
数式では以下のようになります。
$P=\dfrac{1}{2}ρv^2$・・・②
$P$:風から受ける圧力[$Pa$]
$ρ$:空気の密度[$kg/m^3$]
$v$:風速[$m/s$]
空気の密度はほぼ一定と考えると、風から受ける圧力は風速の二乗に比例して大きくなることが分かります。
この圧力の単位は[$Pa$]なので、風を受ける面積が大きいほど受ける力も大きくなります。
風が強い日などは、前かがみになって歩くこともありますよね。
これは風を受ける面積を減らすという意味で有効です。
ちなみに台風のときの風については、以下の記事で解説しています。
抗力係数
風を受ける面が同じ面積でも、形状によって抵抗が大きく感じるということがあります。
例えば、立方体のような形状と円柱のような形状を比較すると、面積が同じでも円柱の方が受ける抵抗が小さくなります。
このような差を考えるために、実験的に求めた係数が抗力係数と呼ばれる値になります。CD値と呼ばれることもあります。
抗力係数を導入数すると、式②は以下のようになります。
$P=C_d\dfrac{1}{2}ρv^2$・・・②’
$C_d$:抗力係数
この抗力係数は、流れ方向から見た形状によって決まります。
そして抗力係数が小さいほど風による圧力の影響を小さくできる事が分かります。
抵抗を受けにくい形状
それでは、どのような形状が抗力係数が小さくなっているのでしょうか。
以下の表に、代表的な形状と抗力係数の値を記載しました。
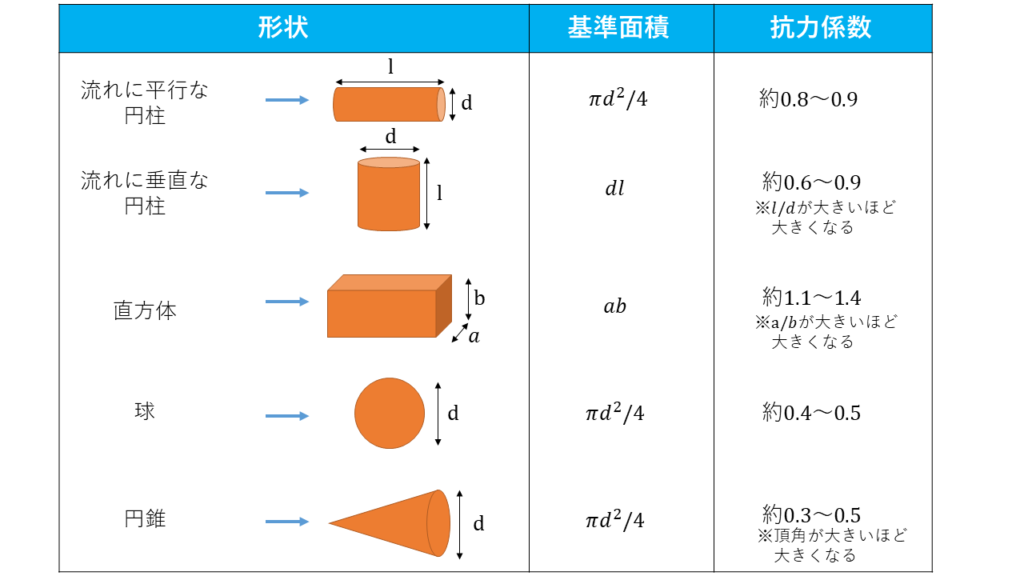
この結果を見ると、球や円錐のような形状にすることで、抗力係数を小さくすることができます。
反対に直方体のように風に対して垂直な壁を作るような形状にしてしまうと、風の影響を大きく受けてしまうので、注意が必要です。
実際の機械での適用例

例えば、新幹線の先頭車両の形状はどうなっているでしょうか?
先端が尖ったような形状になっていると思います。
これは風から受ける影響を小さくするため、抗力係数が小さくなるよう設計されてると言われています。
他にも同様の理由で、飛行機や車なども先端を小さくするような形状が多く見られると思います。
まとめ
いかがだったでしょうか。
今回は風から受ける抵抗について解説してきました。
まとめると以下のようになります。
- 風の抵抗は、風の圧力と面積の積によって決まる
- 風の圧力を小さくするには、球や円錐形などの抗力係数の小さい形状にする必要がある
- 抗力係数の考え方は新幹線などの機械に利用されている






















