層流と乱流の違いとは？【流体力学の基礎解説】

皆さんは層流や乱流という言葉を聞いたことがありますか？

流体力学の世界ではよく聞く言葉かと思いますが、何が違うのでしょうか。

今回は層流と乱流の違いについて解説していきたいと思います。

層流とは

層流とは、流体が層状になって滑らかに流れている状態のことを指します。

速度場が一定で、乱れが少ないことが特徴です。

ゆっくり流れる水道の水が層流の例として挙げられます。

層流と乱流を判別するとき、レイノルズ数という無次元数を用いて表しますが、レイノルズ数は以下の式によって表されます。

一般的にレイノルズ数が2000以下の場合は層流となる場合が多いです。

このとき、式①から考えると、レイノルズ数$Re$が小さくなる時は、密度$ρ$、流速$v$、代表長さ$L$が小さいか、粘度$μ$が大きいときになります。

つまり層流のときは、速度による慣性力よりも粘度による粘性力の方が大きいと考えられます。

乱流とは

乱流とは、流体が不規則で渦を巻くような状態となっていることを指します。

流れに乱れがあり、エネルギーの損失が多いため、流れの挙動が複雑になります。

川の急流や、高速道路を走る車周囲の空気流が例として挙げられます。

一般にレイノルズ数が4000より大きい場合は、乱流とみなされることが多いです。

式①を見ると、分子の値が大きい時にレイノルズ数$Re$が大きく、乱流となりやすいため、速度による慣性力が粘性力よりも大きい状態と考えられます。

層流と乱流の遷移

例えば、パイプの中を流れる水を考えてみます。

このとき、どのくらいの流速で層流から乱流に遷移するのでしょうか。

パイプの直径を代表長さ$L=0.05$[$m$]、$0.1$[$m$]、$0.2$[$m$]、動粘度$ν=1×10^{-6}$[$m^2/s$]は一定として、流速を変えた場合、以下の値となります。

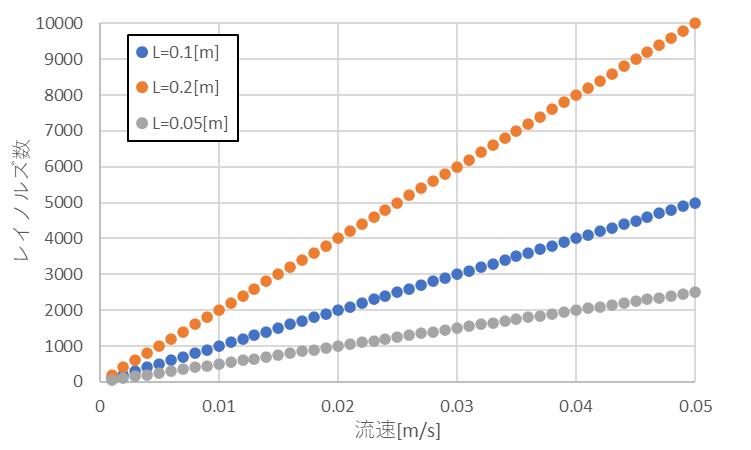
パイプの直径を代表長さ$L$が大きい方が、低い流速でレイノルズ数が大きくなることが分かると思います。

実際の実験では、温度変化や乱流による乱れが発生するため、数式通りにレイノルズ数が変化しないこともありますが、流速が上がるにつれて、レイノルズ数も上がることが分かると思います。

機械設計での扱い

機械設計でも、以下のような場面で層流や乱流を扱うことがあります。

・配管などのパイプ設計

　パイプ内の流れの検討を行います。プラントなどでは高速で流体を運ぶ必要があるため、乱流になりやすいです。

・電子機器の空冷ファンの設計

　電子機器は発熱しやすいので、放熱にファンを使用することもあります。風速が大きいと乱流になります。

・自動車の空気抵抗の設計

　自動車が動いているときは、周囲に風が流れている状態となります。このときの周囲空気は乱流の状態で検討することがあります。

測定時の空気の流速は、以下のような流速計を使うこともあります。

まとめ

いかがだったでしょうか。

今回は層流と乱流について解説してきました。

まとめると以下のようになります。