振動の動吸振器とは？【機械力学的解説】｜機械工学・設計・解説サイト

皆さんは動吸振器という物をご存じでしょうか？

ダイナミックダンパと呼ばれることもありますが、今回は動吸振器の原理について解説していきたいと思います。

Contents

動吸振器の役割
動吸振器有無の比較
実際の動吸振器の例
まとめ

動吸振器の役割

動吸振器とは、物体の動きを抑える性能を持つ物を表しています。

広い意味ではダンパーも動吸振器として扱われることもあります。

今回は振動する物体に対して、ばねや質量を付与して振動を抑えるための構造の事を動吸振器と呼ぶことにします。

振動している物体の中で、最も振動する現象は、共振が発生したときになります。

このときの振動数を共振周波数と呼びますが、共振周波数を変化させるには、物体の質量を変えるか、剛性を変える方法の2通りしかありません。

どちらの方法も材質を変えることに繋がりますので、性能が変わる、部材コストが上がる、入手性悪くなるなどの大きなリスクを伴う可能性があります。

そこで今の装置に部品を追加することで、共振周波数を変えることができる物が動吸振器と呼ばれる機器になります。

動吸振器有無の比較

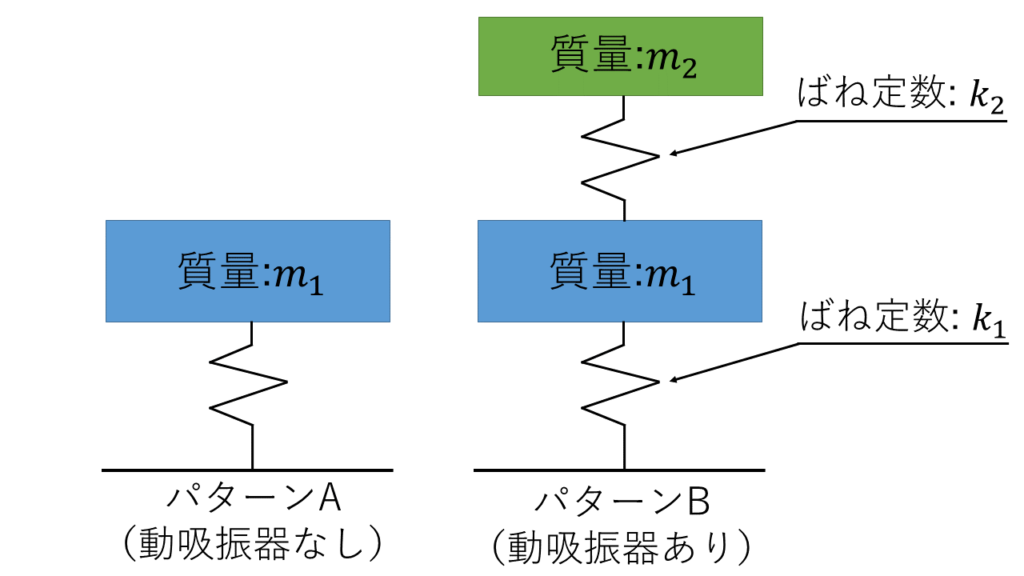
それでは実際にどのくらい違うのかを数値比較してみましょう。

質量 $m$ の物体がばねに固定されて、周期的な振動を加えられる場合を考えてみます。

ばね定数 $k$ のばねのみで固定されているパターンAと動吸振器を追加したパターンBで比較すると、まずパターンAの場合の運動方程式は以下のようになります。

数式

$m \frac{d^{2} x}{d t^{2}} + k x = F ・ c o s ω t$

$m$ ：物体の質量[ $k g$ ]

$x$ ：物体の変位[ $m$ ]

$t$ ：時間[ $s$ ]

$k$ ：ばね定数[ $N / m$ ]

$F$ ：荷重[ $N$ ]

$ω$ ：角振動数[ $/ s$ ]

一方でパターンBの場合は以下のようになります。

数式

$m_{1} \frac{d^{2} x_{1}}{d t^{2}} + (k_{1} + k_{2}) x_{1} - k_{2} x_{2} = F ・ c o s (ω t)$

$m_{2} \frac{d^{2} x_{2}}{d t^{2}} - k_{2} x_{1} + k_{2} x_{2} = 0$

$m_{1}$ ：物体の質量[ $k g$ ]

$m_{2}$ ：動吸振器の質量[ $k g$ ]

$x_{1}$ ：物体の変位[ $m$ ]

$x_{2}$ ：動吸振器の変位[ $m$ ]

$k_{1}$ ：物体固定用ばねのばね定数[ $N / m$ ]

$k_{2}$ ：動吸振器用ばねのばね定数[ $N / m$ ]

この数式を解いた結果を比較していきます。

以降は具体例として $m_{1} = k g$ 、 $k_{1} = 3 N / m$ 、 $F = 5 N$ とします。

共振周波数の違い

まずは共振周波数の違いです。

各振動数を変化させたときの変位を以下のグラフに示します。このとき $m_{2} = 0.5 k g$ 、 $k_{2} = 1 N / m$ としています。

縦軸が変位で横軸が角振動数を表しています。

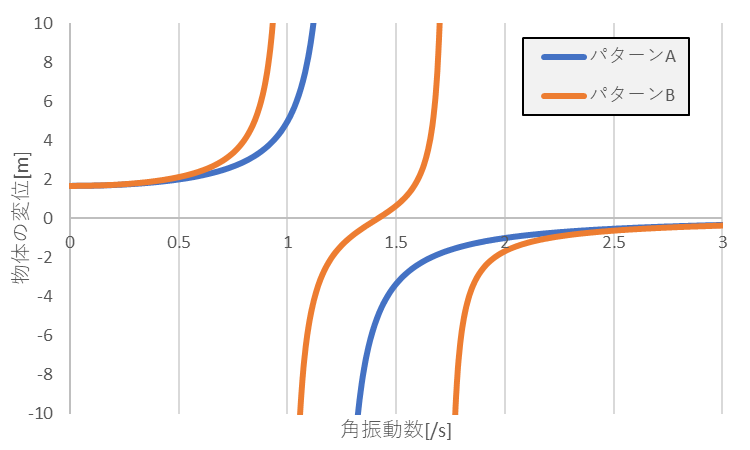
この結果を見ると、パターンAでの共振する角振動数は約 $1.2 / s$ 付近なのに対し、パターンBでは約 $1 / s$ と $1.7 / s$ の2つが存在します。

このことから、動吸振器を用いることで共振する振動数を変化させることができます。

ただし、共振点が2つに増えてしまうので、今までは問題なかった部分で共振が発生してしまうこともあります。

動吸振器の定数による違い

ここで、動吸振器の定数を大きくするとどうなるのでしょうか。

前述のパターンBのパラメータに対して、質量 $m_{2}$ を2倍にしたときと、ばね定数 $k_{2}$ を2倍にしたときの結果を以下のグラフに示します。

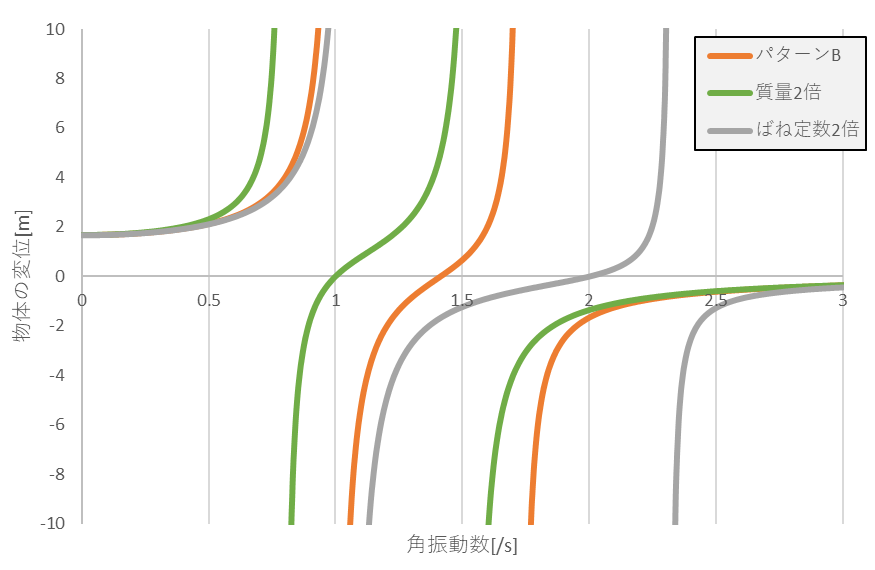
パターンBの元の結果と比較すると、質量を大きくすることで共振する周波数は小さくなります。

一方でばね定数を大きくした場合は、2か所目の共振点を見ると、振動数が大きくなっていることが分かります。

このように、ばね定数を大きくすることで、共振する周波数を大きくすることが可能です。

数式による検討

ここで数式についても少し触れておきます。

動吸振器の運動方程式を $x 1$ について解くと以下のようになります。

数式

$x_{1} = \frac{(- m_{2} ω^{2} + k_{2}) F ・ c o s (ω t)}{(- m_{1} ω^{2} + k_{1} + k_{2}) (- m_{2} ω^{2} + k_{2}) - k_{2}^{2}}$

この式の分母が0になるときの $ω$ が共振点として現れます。

$ω$ についての四次方程式となりますが、このときパラメータとして関わってくるのが、 $m_{1}$ 、 $m_{2}$ 、 $k_{1}$ 、 $k_{2}$ の4種類あります。

つまりどのパラメータを調整しても、共振する周波数には影響を与えてしまいます。

実際の動吸振器の例

実際の製品でも、様々なところに動吸振器が使われています。

例としては、ビルなどに使われている制振構造が挙げられます。

制振構造については、以下の記事で紹介しています。

また、もっと身近な例だと、ゴムシートや車のタイヤなども振動を吸収する部品としては挙げられます。

この場合は、動吸振器側にばねだけでなくダンパーまで含めた、粘性減衰付動吸振器の構造となっていることもあります。

まとめ

いかがだったでしょうか。

今回は動吸振器について解説してきました。

まとめると以下のようになります。

まとめ

動吸振器は振動を抑制するために用いられる
付与する質量とばね定数の値によって共振周波数を調整可能
動吸振器によって共振する周波数が増えるので、注意が必要

振動の動吸振器とは？【機械力学的解説】

動吸振器の役割