ダンパーのある共振って?【機械力学的解説】

皆さんは共振という現象をご存じでしょうか。
ある振動数のときに振幅が大きくなってしまう現象のことですが、詳しくは以下の記事で解説しています。
上記の記事では、ばねで繋がれた物体の共振を考えてきました。
今回はダンパーとばねによって接続された物体の共振点がどのように変わるのかを解説していきたいと思います。
そもそもダンパーとは?
ダンパーとは、運動エネルギーを吸収できる機構のことを指しますが、詳細は以下の記事で解説しています。
運動方程式
ここでは、ダンパーなしの場合とダンパーありの場合でそれぞれ検討していきます。
ダンパーなしの場合
ダンパーなしの場合で、周期的に荷重が発生する場合、運動方程式は以下のようになります。
$m\dfrac{d^ 2x}{dt^ 2}+kx=Fcos(ωt)$
ここでの特殊解は以下のようになります。
$x_f=\dfrac{F}{-mω^2+k}cos(ωt)$
グラフで表すと以下のようになります。
縦軸は変位を、横軸は時間を表しています。

ダンパーありの場合
次に上記の図のように、ばねとダンパーを並列につないだ場合で、周期的に荷重が発生する場合について考えていきます。
このときの運動方程式は以下のようになります。
$m\dfrac{d^ 2x}{dt^ 2}+c\dfrac{dx}{dt}+kx=Fcos(ωt)$
このときの解は以下のようになります。
$x_f=\dfrac{F}{(-mω^2+k)^2+(cω)^2}((-mω^2+k)cos(ωt)+(cω)sin(ωt))$
グラフで表すと以下のようになります。
荷重に対して大きく振幅が減少していることが分かると思います。

共振の有無
ここで角速度の変化による違いを考えていきます。
縦軸は変位、横軸は角速度を表しています。
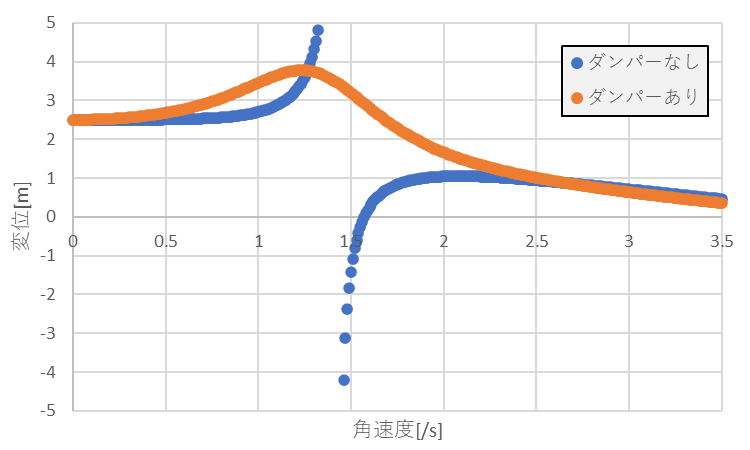
共振時の周波数である$1.3/s$ 付近では、ダンパーなしの場合は発散しています。
しかしダンパーありの場合では、少し変位が大きくなるだけで発散しないことが分かります。
このようにダンパーを用いることで共振時の振動を大きく抑えることが可能です。
減衰係数による違い
それでは、減衰係数の値を変えるとどうなるかを考えていきます。
減衰係数の値を変更したときのグラフを以下に示します。

このように減衰係数の値を0に近づけるにつれてダンパーなしの状態に近づいていきます。
一方で減衰係数の値を大きくすることで、共振時でも変位を抑えることが可能です。
まとめ
いかがだったでしょうか。
今回はダンパーあるの場合の共振について紹介してきました。
まとめると以下のようになります。
- ダンパーの有無によって振幅を抑えられる
- ダンパーを追加することで、共振時の振幅の発散をなくすことが可能
- 減衰係数の大きいダンパーを用いることで、より振幅を抑えられる






















