皆さんは荷重の時間変化を意識していますか。
時間変化する荷重の代表例には、インパルス荷重、ステップ荷重、ランプ荷重がありますが、どのように違うのでしょうか。
今回は、荷重の違いについて解説していきたいと思います。
時間変化の重要性
機械に作用する荷重は、大きさだけでなく時間的な変化によっても影響が異なります。
例えば、最大荷重が同じであっても、急に加わるか、ゆっくり加わるかで発生する応力や変形は異なります。
設計時にはこの時間変化を理想化して計算します。
この理想化の代表例がインパルス荷重・ステップ荷重・ランプ荷重の3つになります。
インパルス荷重とは？
インパルス荷重は、短時間に作用する大きな荷重のことを指します。
短時間で発生する荷重のため、力積(Impulse)で評価されます。
以下のような数式で表されます。
$F(t)= \left\{\begin{array}{rr}F_0&(t=0)\\0& (t≠0)\end{array}\right.$
$F(t)$：荷重関数
$t$：時間
$F_0$：一定荷重
グラフで表すと以下のようになります。
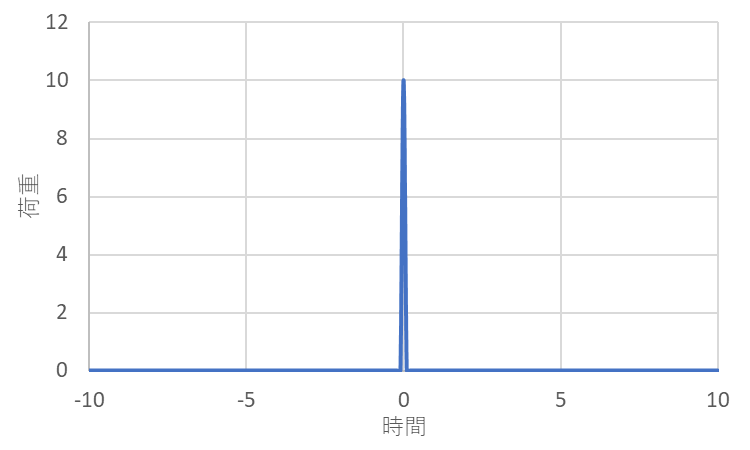
ある時間のときのみ荷重が発生していることが分かると思います。
実際の現象に当てはめてみると、ハンマーで部品を叩く瞬間や、落下物が当たる瞬間に適用されます。
ステップ荷重とは？
ステップ荷重は、瞬間的に一定値まで増加し、そのまま一定の荷重がかかり続ける状態を指します。
数式では以下のように表されます。
$F(t)= \left\{\begin{array}{rr}0&(t<0)\\F_0&(t≧0)\end{array}\right.$
$F(t)$：荷重関数
$t$：時間
$F_0$：一定荷重
グラフで表すと以下のようになります。
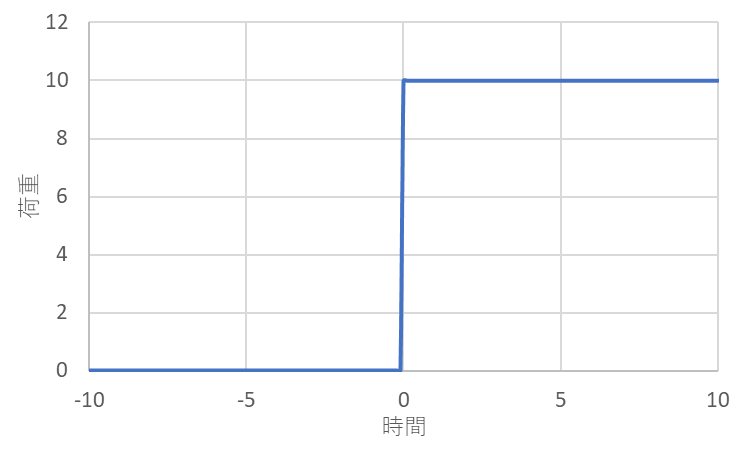
ある瞬間から荷重が発生し続けていることが分かると思います。
実際には、一定質量の荷物を載せるときなどに適用されます。
ランプ荷重とは？
ランプ荷重とは、一定の速度で荷重が増加する状態のことを指します。
数式では以下のように表されます。
$F(t)= \left\{\begin{array}{rr}0&(t<0)\\kt&(0≦t≦t_1)\\F_0&(t_1<t)\end{array}\right.$
$F(t)$：荷重関数
$t$：時間
$k$：定数
$t_1$：一定時間
$F_0$：一定荷重
グラフで表すと以下のようになります。
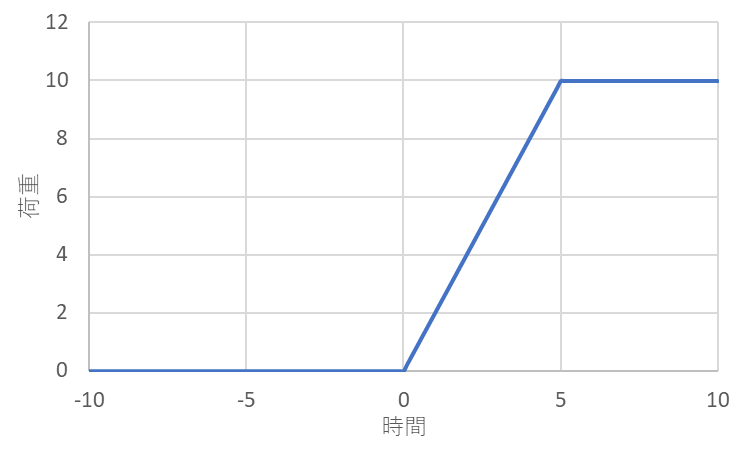
グラフでは$t_1$を5としていますが、線形的に荷重が増加している様子が分かると思います。
ランプ荷重は、モーターのトルクが一定加速度で増加していくようなときに使用されます。
違いの比較
違いをまとめると以下の表のようになります。
| 項目 | インパルス荷重 | ステップ荷重 | ランプ荷重 |
| 荷重の加わり方 | 瞬間的 | 瞬間的 | 徐々に増加 |
| 印加後の荷重 | 0 | 一定荷重 | 一定荷重 |
| 荷重の例 | ハンマーによる衝撃 | 荷物の搭載荷重 | トルクの一定増加 |
設計時の注意点
設計時には、以下の点に気を付ける必要があります。
インパルス荷重はピーク時の荷重が非常に大きいです。
材料強度がピーク荷重に耐えられるかの検討が必要です。
ステップ荷重は瞬間的な応答が発生するため、減衰要素の影響があります。
ランプ荷重はゆっくりですが、最大荷重到達後の耐力の確認が必要となります。
まとめ
いかがだったでしょうか。
今回は、インパルス荷重、ステップ荷重、ランプ荷重について解説してきました。
まとめると以下のようになります。
- インパルス荷重は瞬間的な衝突を表す
- ステップ荷重は急に一定の荷重がかかる状態を表す
- ランプ荷重は徐々に荷重がかかる状態を表す
