振動の応答倍率とは?【機械力学の基礎解説】

皆さんは応答倍率という言葉を聞いたことはありますか?
振動の解析や評価を行ったことがある方は、聞いたことがあるかもしれません。
今回は振動の応答倍率について解説していきたいと思います。
応答倍率の考え方
応答倍率とは、振動の入力の大きさに対して、出力が何倍になっているかを表した値のことを指します。
例えば、与えた振動の加速度が3[$m/s^2$]で、物体の加速度が6[$m/s^2$]だったとき、応答倍率は2倍となります。
加速度ではなく、変位で計算することもあります。
実際の測定では、加速度センサーを貼り付けて、既知の振動を加えることで応答倍率を計算できます。
応答倍率の計算例
ばね系の振動の場合
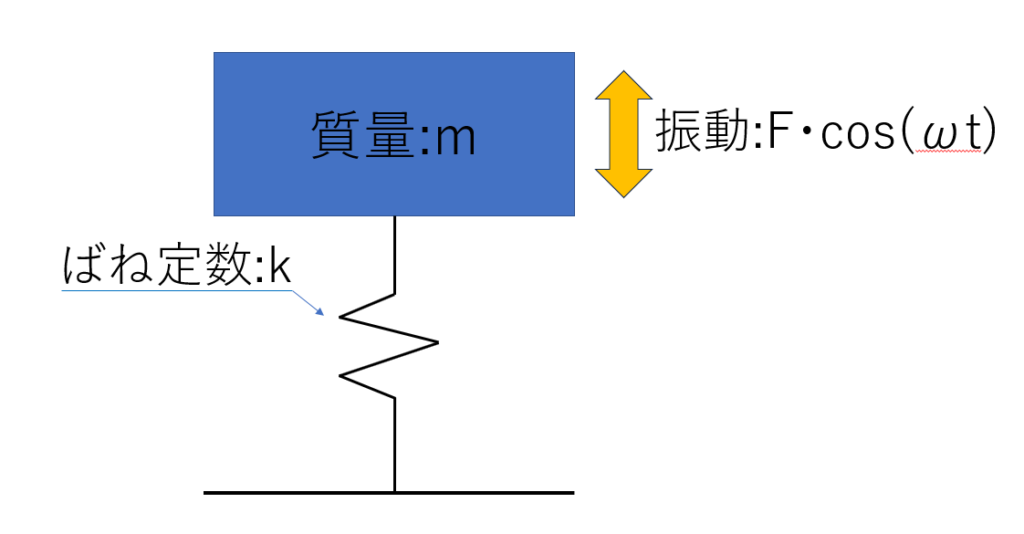
ばねのみによって支持されている系を考えてみましょう。
このとき、運動方程式は以下のようになります。
$m\dfrac{d^2x}{dt^2}+kx=Fcos(ωt)$・・・①
この式①を変位$x$について解くと、以下のようになります。
$x=\dfrac{F}{k-mω^2}cos(ωt)$・・・②
この結果から、応答倍率を求めることができます。
応答倍率は、出力される変位を入力の変位で割った値となります。
まとめると以下のようになります。
入力の変位:$\dfrac{F}{k}cos(ωt)$
出力される変位:$\dfrac{F}{k-mω^2}cos(ωt)$
応答倍率:$\dfrac{k}{k-mω^2}$・・・③
ばね・ダンパー系の振動の場合
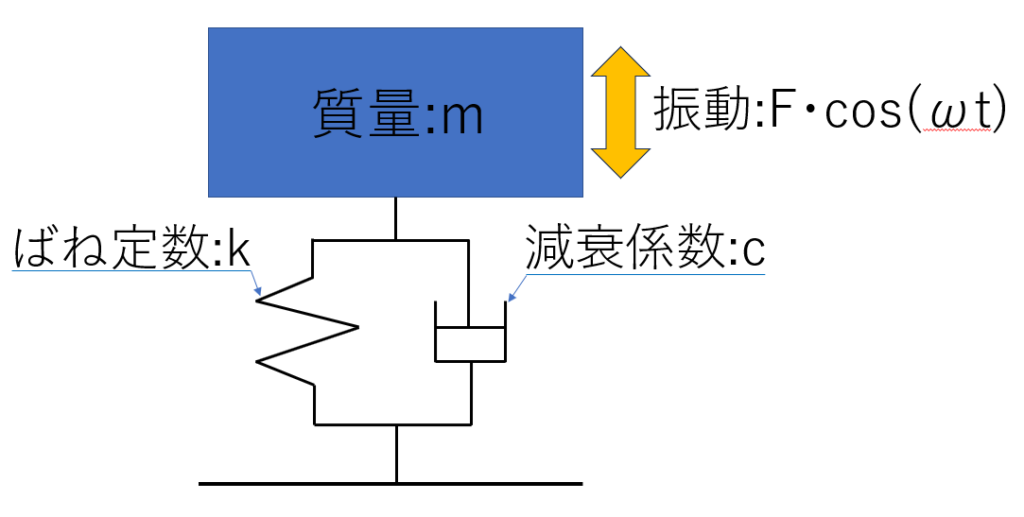
次はばねとダンパーによって支持されている系について考えてみます。
このときの運動方程式は以下のようになります。
$m\dfrac{d^2x}{dt^2}+c\dfrac{dx}{dt}+kx=Fcos(ωt)$・・・④
この式④を変位$x$について解くと、以下のようになります。
$x=\dfrac{F}{(-mω^2+k)^2+(cω)^2}((-mω^2+k)cos(ωt)+(cω)sin(ωt))$・・・⑤
式③と同様に出力される変位を入力の変位で割った値によって応答倍率を求めます。
まとめると以下のようになります。
応答倍率:$\dfrac{k}{(-mω^2+k)^2+(cω)^2}((-mω^2+k)+(cω)tan(ωt))$・・・⑥
応答倍率を小さくするには?
まず、ばね系の振動を考えてみます。
式③を見てみると、分子と分母にばね定数$k$が存在するため、
約分すると以下のようになります。
応答倍率:$\dfrac{1}{1-\dfrac{m}{k}ω^2}$・・・③’
分母が大きいほど応答倍率を小さくできるので、
$1-\dfrac{m}{k}ω^2$を最大化する必要があります。
つまり$\dfrac{m}{k}ω^2$が小さい値となるときに応答倍率を小さくできます。
大きく分けて2つのパターンが考えられます。
- 質量$m$を小さくする
- ばね定数$k$を大きくする
固有角振動数$ω$を一定値とした場合、$m$と$k$を変数としたときの応答倍率は以下のグラフのようになります。
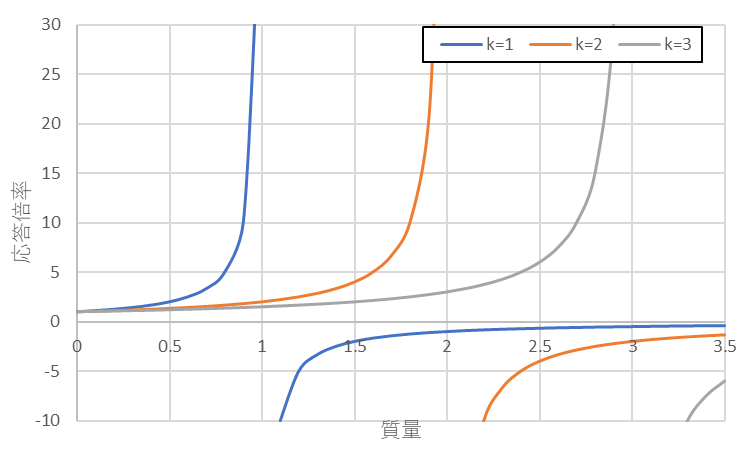
質量$m$とばね定数$k$の比率によって応答倍率の大きさが変化していることが分かると思います。
これは応答倍率の分母の値が0となり、発散するために起こります。
このように応答倍率の値が急激に上がっている現象を共振と呼びます。
まとめ
いかがだったでしょうか。
今回は、振動における応答倍率について解説してきました。
まとめると以下のようになります。
- 応答倍率は、入力と出力の比によって求められる
- 応答倍率の値は、質量を小さくするか剛性を大きくすることで小さくできる
- 応答倍率の値が発散することで共振が生じる





















