梁の共振周波数と固定方法の関係【機械力学的解説】

皆さんは共振する部品の固定方法について考えたことはありますか?
共振が発生するとき、固定方法の違いによって結果が変わってくると思います。
今回は固定方法によってどのくらい共振周波数が変わってくるのかを解説していきたいと思います。
梁の運動方程式
梁の振動についての運動方程式は以下のように表されます。
$\dfrac{∂^2v}{∂t^2}+\dfrac{EI}{ρA}\dfrac{∂^4v}{∂x^4}=0$・・・①
$v$:梁の変位[$m$]
$t$:時間[$s$]
$x$:梁の位置[$m$]
$E$:梁のヤング率[$Pa$]
$I$:梁の断面二次モーメント[$m^4$]
$ρ$:梁の密度[$kg/m^3$]
$A$:梁の断面積[$m^2$]
この数式は一般解を求めることができます。
$v=V(x)・e^{jωt}$・・・②
ただし、以下の式を満たす。
$V(x)=C_1coshλx+C_2sinhλx+C_3cosλx+C_4sinλx$・・・③
$λ^4=\dfrac{ω^2ρA}{EI}$・・・④
$C_1~C_4$:固定方法によって決まる定数
このとき、$C_1~C_4$が固定方法によって決まります。
そして$C_1~C_4$の値よりλの値が求まることで、式④から固有円振動数$ω$を得ることができます。
各固定での固有円振動数
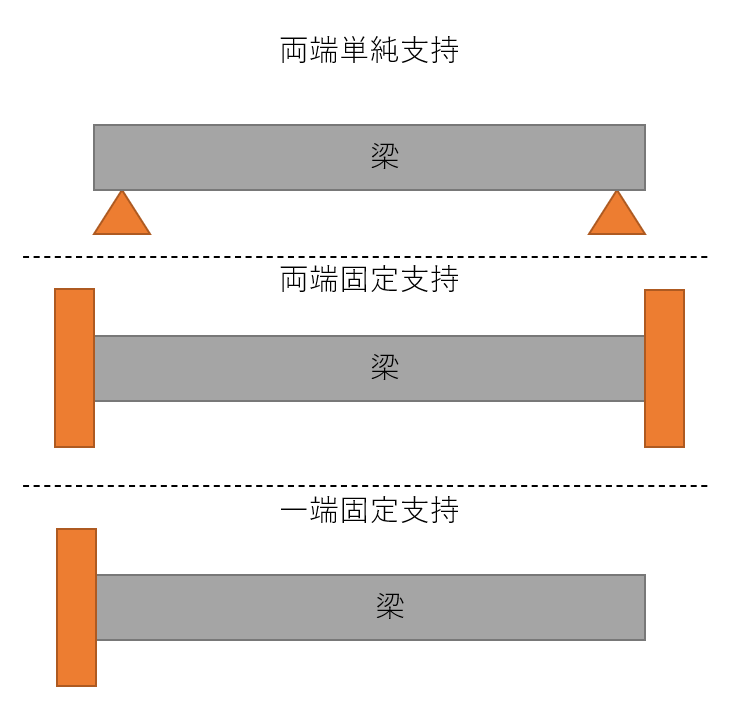
それでは、各固定方法での固有円振動数を求めていきます。
この固有円振動数が分かれば、共振周波数を求める事も可能です。
ここでは設計でよく用いる両端単純支持、両端固定支持、一端固定支持(片持ち梁)の場合の3パターンを考えてみます。
両端単純支持の場合
両端支持の場合、梁の両端で変位とモーメントが0となります。
このことから式③を整理すると、以下の値を得ることができます。
$sinhλl・sinλl=0$・・・⑤
⇔$λl=π,2π,3π・・・nπ$・・・⑥
$l$:梁の長さ[$m$]
式④に式⑥から求まる$λ$を代入することで、固有円振動数$ω$の一般解が求まります。
両端固定支持の場合
両端固定支持の場合、梁の両端で変位とたわみ角が0になります。
ここから式③を整理すると以下の値を得ることができます。
$coshλl・cosλl=1$・・・⑦
⇔$λl=4.73,7.85,11.0・・・$・・・⑧
式⑦は代数的に解けないため、近似値を式⑧に示しました。
両端単純支持の場合と同様に、式④に代入することで、固有円振動数$ω$の一般解が求まります。
一端固定支持の場合
一端固定支持の場合は、両端で境界条件が異なります。
梁の片方の端では、変位とたわみ角が0になり、反対側ではモーメントとせん断力が0になります。
このことから以下の数式が求まります。
$coshλl・cosλl=ー1$・・・⑨
⇔$λl=1.88,4.69,7.85・・・$・・・⑩
式⑨も代数的に解けないため、近似値を式⑩に示しました。
固定方法の比較
各固定方法での固有振動数をまとめると以下のようになります。
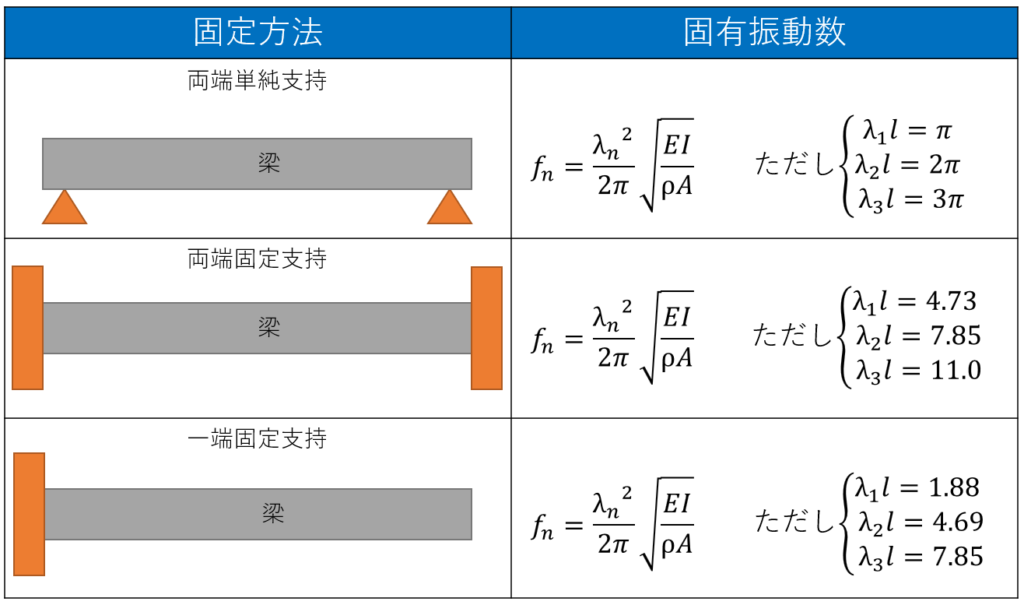
$π≒3.14$であることを考慮すると、一端固定→両端単純支持→両端固定支持と固定方法を強固にしていくにつれて、固有振動数が大きくなることが分かります。
つまりこの結果から考えると、梁の固有振動数を大きくするには以下の方法が挙げられます。
- 固定方法を強固にする
- ヤング率を大きくする
- 断面二次モーメントを大きくする
- 密度を小さくする
- 断面積を小さくする
もし梁が曲げ方向で共振してしまった場合は、上記の方法による対策が考えられます。
まとめ
いかがだったでしょうか。
今回は梁の曲げ方向の共振について解説してきました。
まとめると以下のようになります。
- 曲げ方向の固有円振動数は固定方法によって異なる
- 固定方法を強固にするほど共振周波数も大きくなる
- 固定方法以外にも、梁の物性によって共振周波数が変わる






















