耐振・免振・制振の違いって?【機械力学的解説】

皆さんは振動の抑え方の違いをご存じでしょうか。
家を買うときなどは「耐震構造」や「免震構造」などの記載がありますが、
どのような違いがあるのでしょうか。
今回は振動対策構造の違いについて紹介したいと思います。
表記違いについて
既にお気付きかもしれませんが、「耐震」と「耐振」の二種類の表記があります。
この表記にはもちろん違いがあります。
「震」の文字を使った耐震とは、地震に対応できる構造という意味です。
一方で「振」の文字を使った耐振は、振動に対応できる構造という意味です。
今回は地震以外の様々な振動に対応するという意味で、「耐振」という文字を使用させて頂きます。
構造の種類

振動を対策する構造は3種類あります。
耐振構造
まず挙げられるのは耐振構造です。
これは文字通り、振動に耐える構造のことを指しています。
具体的には、柱の数を増やす、柱を太くするなどの方法が考えられます。
免振構造
免振構造とは振動吸収して揺れを伝えにくくする構造のことを指しています。
例えば、地震対策で本棚の角にゴムマットを敷いていることを見たことはないでしょうか。
これが免震構造です。
地震などの振動を、ゴムマットで吸収しているため、本棚に直接伝わる振動を抑えています。
機械工学や建築の世界では、このような機能を持つ台のことを免振台と呼びます。
制振構造
制振構造とは、振動を制御する構造で、耐振構造と免振構造の中間のような構造です。
これは免振台のような台で振動を吸収するのではなく、構造の中にダンパーを入れて、構造の中で振動を吸収する構造です。
ダンパーについては以下の記事で解説しています。
共振時の違い
ここで、耐振、免振、制振がそれぞれどのように異なるかを考えてみます。
検討モデル
基本の検討モデルとして、2自由度の質点の振動を考えます。
上側にある質点は構造物を、下にある質点は台を表しています。
荷重は地面に周期的な荷重のみが加わることとし、重力の影響は無視します。
通常の場合

2自由度の強制振動の場合、数式は以下のように表されます。
$m_1\dfrac{d^ 2x_1}{dt^ 2}+(k_1+k_2)x_1-k_2x_2=Fcos(ωt)$
$m_2\dfrac{d^ 2x_2}{dt^ 2}-k_2x_1+k_2x_2=0$
この数式を$x_2$について解くと、以下のようになります。
$x_2=\dfrac{k_2Fcos(ωt)}{m_1m_2(ω^2-ω_1^2)(ω^2-ω_2^2)}$・・・①
ただし、$ω_1$と$ω_2$は以下の値とする
$ω_1=\sqrt{\dfrac{1}{2}}\sqrt{{\dfrac{k_1+k_2}{m_1}+\dfrac{k_2}{m_2}-\sqrt{(\dfrac{k_1+k_2}{m_1}+\dfrac{k_2}{m_2})^2-\dfrac{4k_1k_2}{m_1m_2}}}}$
$ω_2=\sqrt{\dfrac{1}{2}}\sqrt{{\dfrac{k_1+k_2}{m_1}+\dfrac{k_2}{m_2}+\sqrt{(\dfrac{k_1+k_2}{m_1}+\dfrac{k_2}{m_2})^2-\dfrac{4k_1k_2}{m_1m_2}}}}$
耐振構造の場合

耐振構造の場合は、単純に剛性が大きくなると考えられるので、通常の場合の$k_2$の値が大きくなります。
今回は簡単のため、支えているばねが2本並列に増えると考えます。
数式は$k_2$の部分を$2k_2$として①の式で求めます。
免震構造の場合

免震構造の場合は、台座と地面の間にダンパが入っていると仮定して考えます。
このとき、運動方程式は以下のようになります。
$m_1\dfrac{d^ 2x_1}{dt^ 2}+c_1\dfrac{dx_1}{dt}+(k_1+k_2)x_1-k_2x_2=Fcos(ωt)$
$m_2\dfrac{d^ 2x_2}{dt^ 2}-k_2x_1+k_2x_2=0$
この数式を$x_2$について解くのですが、煩雑なので以下のように表現します。
$x_2=\sqrt{X^2+Y^2}cos(ωt-Φ)$・・・②
ただし、各文字$X、Y、Φ$は以下の値を満たす
$X=Re(Z)$
$Y=Im(Z)$
$Φ=arctan(-\dfrac{Y}{X})$
$Z=\dfrac{k_2F}{((-m_1ω^2+k_1)(-m_2ω^2+k_2)-m_2k_2ω^2)-jωc_1(-m_2ω^2+k_2)}$
(実運用上は、数式の変形が全て完了していなくても、エクセルやプログラム言語で計算することが可能です。)
制振構造の場合

制振構造の場合は、台座と構造物の間にダンパが入っていると仮定します。
(本来は柱と柱の間にもダンパが入ることもあるので、さらに複雑になると思います。)
この場合の運動方程式は以下のようになります。
$m_1\dfrac{d^ 2x_1}{dt^ 2}+c_2\dfrac{dx_1}{dt}-c_2\dfrac{dx_2}{dt}+(k_1+k_2)x_1-k_2x_2=Fcos(ωt)$
$m_2\dfrac{d^ 2x_2}{dt^ 2}-c_2\dfrac{dx_1}{dt}+c_2\dfrac{dx_2}{dt}-k_2x_1+k_2x_2=0$
免振よりもさらに複雑な式になりました。
この数式をについて解くのですが、引き続き煩雑なので以下のように表現します。
$x_2=\sqrt{X^2+Y^2}cos(ωt-Φ)$・・・③
ただし、各文字$X、Y、Φ$は以下の値を満たす
$X=Re(Z)$
$Y=Im(Z)$
$Φ=arctan(-\dfrac{Y}{X})$
$Z=\dfrac{(jωc_2+k_2)F}{((m_1ω^2-k_1)(m_2ω^2-k_2)-m_2k_2ω^2)+jωc_2((m_1+m_2)ω^2-k_1)}$
結果の比較
ここで①~③に値を代入したときの結果を以下に示します。
各定数は$F=5N、m_1=2kg、m_2=1kg、c_1=c_2=2N・s/m、k_1=k_2=4N/m$としました。
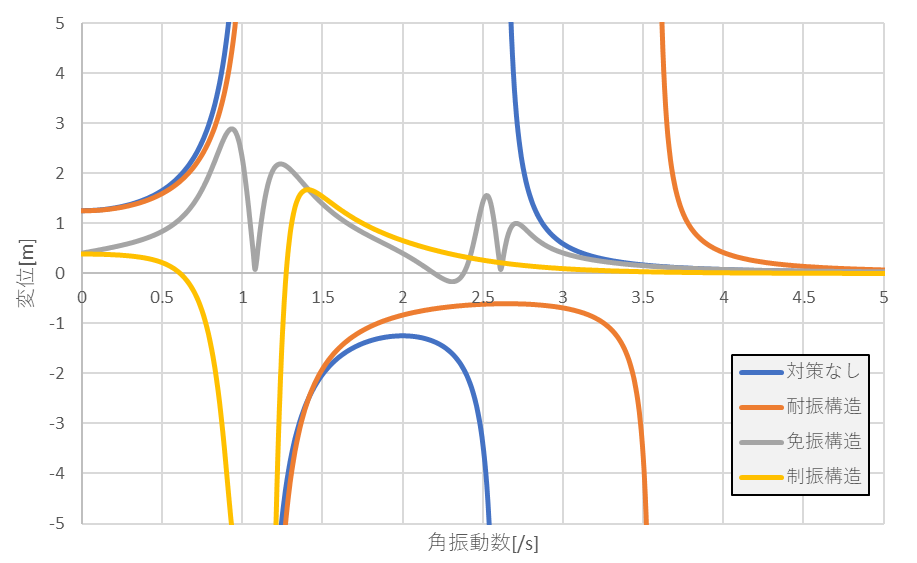
何も対策していない状態(青色プロット)だと、共振点は約$1.2/s$と$2.6/s$の2か所あることが分かります。
ここで対策なし(青色プロット)と耐振構造(橙色プロット)を比較すると、2回目の共振する振動数が大きくなるため、共振点をずらすことが可能です。
一方で免震構造(灰色プロット)と比較すると、ダンパの効果が大きく、共振点でも大きく変位せずに抑えられています。
さらに制振構造(黄色プロット)では、1回目の共振点では大きく共振していいるものの、2回目の共振は発生すらしていない状態です。
このように、各対策でメリットが異なるので、コストと共振を抑える目的をよく相談して決めることが重要です。
まとめ
いかがだったでしょうか。
今回は振動対策構造について紹介してきました。
まとめると以下のようになります。
- 地震の対策には、耐”震”、振動の対策には耐”振”という表記になる
- 振動の対策には、耐振、免振、制振の3つがある
- 対策によって挙動が異なるので、コストと目的によって使い分けることが必要





















