熱い部品を早く冷ます方法は?【伝熱工学的解説】

皆さんはスマホやPCを長時間使っていて、気付いたら熱くなっていたという経験はありますか?
熱くなってしまったら動作も遅くなるし、持っていることも大変ですよね。
ところで放熱時間を短くするにはどうすればいいのでしょうか。
今回は伝熱工学的に、放熱時間を短くする方法を解説していきたいと思います。
放熱時間の求め方
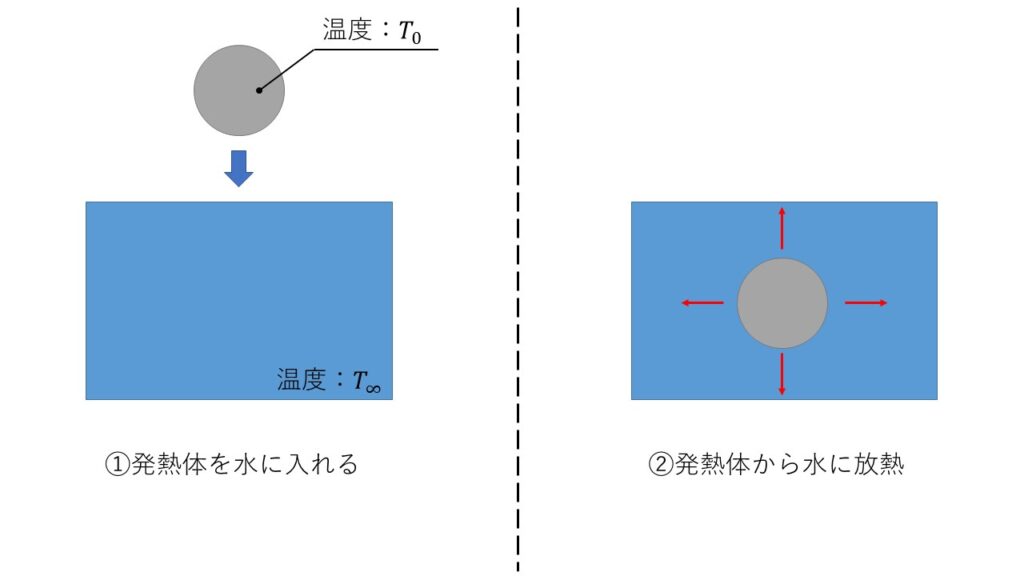
放熱する時間を求めるため、簡単にモデル化して考えます。
高温の鉄球を、温度一定の水の中に入れた場合を仮定すると、鉄球の温度は以下の式で表されます。
$T(t)=T_0+(T_∞-T_0)(1-e^{-\dfrac{t}{τ}})$
$T(t)$:t秒後の物体の温度[$K$]
$t$:経過時間[$s$]
$T_0$:物体の初期温度[$K$]
$T_∞$:水の温度(終端温度)[$K$]
$τ$:時定数[$s$]
このとき$T(t)=T_∞$になったときが、完全に鉄球が冷め切ったと考えることができます。
ここで、時間を短くするために重要なパラメータが時定数$τ$です。
$τ$の値のみ変更したときの温度を以下のグラフに示します。
$T_0=373K(100℃)$、$T_∞=293K(20℃)$としたときの結果になります。
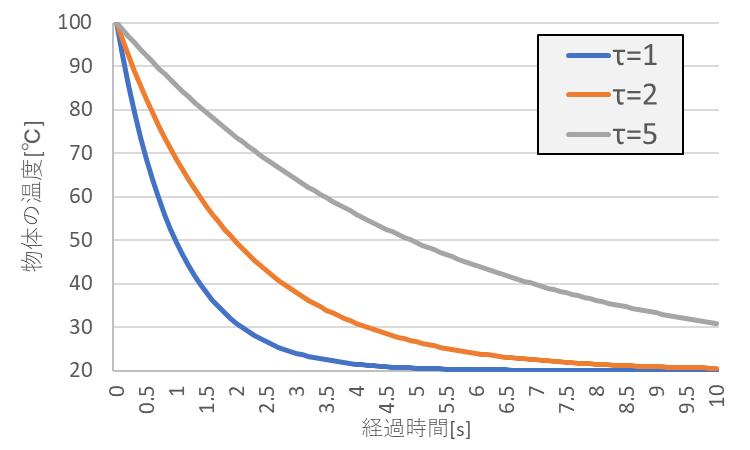
この結果から見ると、時定数$τ=1s$のときは6秒程度で温度が収束していますが、$τ=5s$のときは10秒経っても収束していません。
つまり物体を早く冷ますためには、時定数を小さくすることが必要になります。
時定数とは?
時定数とは、熱平衡状態に達するために必要な時間の目安を表したものです。
終端まで約63.2%の温度変化させるのに必要な時間と言われています。
時定数は以下の式によって求まります。
$τ=mc・\dfrac{1}{hA}$
$m$:物体の質量[$kg$]
$c$:物体の比熱[$J/kg・K$]
$h$:物体間の熱伝達率[$W/Km^2$]
$A$:物体の表面積[$m^2$]
この数式の右辺の1つ目$mc$は熱容量と呼ばれ、物体の温度を1度上げるために必要な熱量を示しています。
2つ目の$\dfrac{1}{hA}$は熱抵抗と呼ばれ、熱の伝わりにくさを表しています。
熱抵抗については以下の記事でも解説しています。
数式より時定数とは、熱容量と熱抵抗の積によって表されていることが分かると思います。
放熱時間を短くする方法
数式を考えると、熱容量または熱抵抗の値を下げれば、時定数の値も小さくすることができます。
具体的には、以下の4つの方法が考えられます。
- 物体の質量$m$を小さくする
- 物体の比熱$c$を小さくする
- 物体間の熱伝達率$h$を大きくする
- 熱移動する表面積$A$を大きくする
例えば、物体の質量$m$や比熱$c$を小さくするには、適用する材料を変更し、密度の小さい物や比熱の小さい材料を適用する、という方法が考えられます。
3点目の物体間の熱伝達率を大きくするには、周囲の流体を変更する・風を流して冷却するという方法が挙げられます。
そして4点目の方法は部材自体を大きくして、空気と触れる面積を大きくするという方法があります。
冷却したい機械の大きさや性能に合わせて、適切な冷却方法を選択しましょう。
まとめ
いかがだったでしょうか。
今回は熱くなった部品を早く冷却する方法について解説してきました。
まとめると以下のようになります。
- 物体が冷却する時間は、時定数によって決まる
- 時定数は熱容量と熱抵抗の積によって表される
- 早く冷やすためには、物体の質量、比熱、熱伝達率、表面積を調整する





















