機械の固有振動数と共振の考え方【機械力学の基礎解説】

機械構造物や回転体の設計において、振動は避けて通れない現象です。
振動を放っておくと、強度や機械の寿命に悪影響を与えてしまいます。
今回は、機械の固有振動数と共振について解説していきたいと思います。
機械振動の基本モデル
振動系の評価では、振動の『自由度』を正しく理解することが重要です。
以下のような違いがあります。
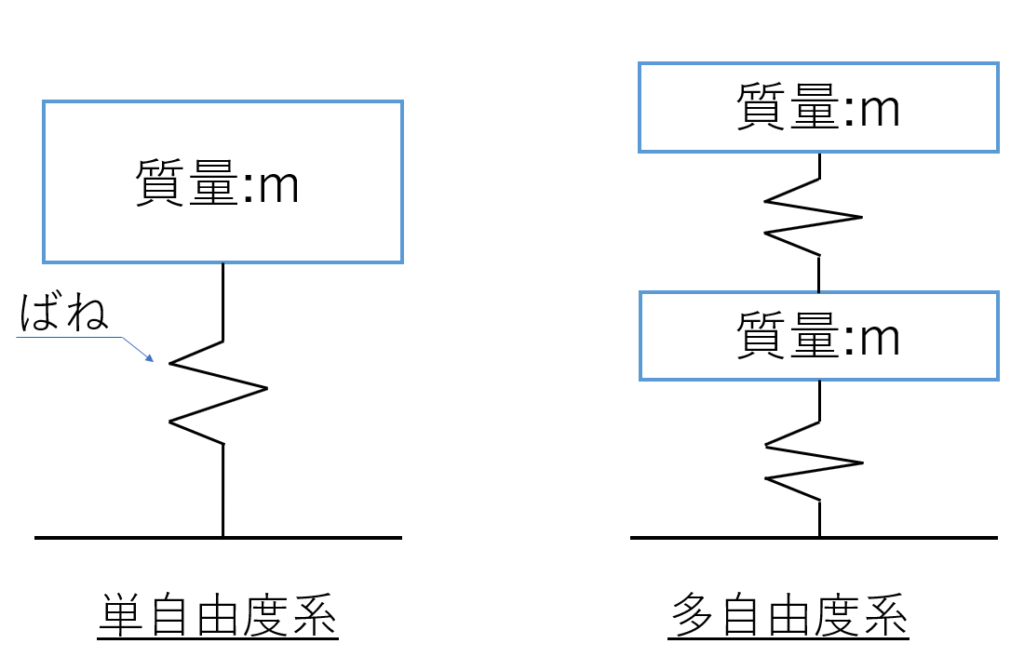
- 単自由度系:軸方向の単純なばね-質量系
- 多自由度系:複雑なフレームや多軸系
振動では、この自由度の数だけ、固有振動数が存在します。
つまり自由度を把握しておかないと、何回共振が発生するか分かりません。
自由振動の場合は、構造物の質量マトリクス$M$と剛性マトリクス$K$を用いて固有値解析を行います。
以下の式で求めることができます。
$(K-Mω^2)Φ=0$
$K$:剛性マトリクス
$M$:質量マトリクス
$ω$:固有振動数[$rad/s$]
$Φ$:固有モードベクトル
例えば、2自由度系であれば、剛性マトリクス・質量マトリクスはそれぞれ2×2のマトリクスとなります。
実際の設計では、単自由度よりも多自由度の共振解析が多くなります。
固有振動数の意味
固有振動数は、部品や機械全体の固有の周期を示します。
この値が、外部から加わる振動数と一致すると、振動が増大してしまいます。
つまり、他自由度系の場合は、固有振動数が多いため、共振が発生するリスクが増大します。
前述の式から考えると、機械の質量と剛性が固有値に影響していることが分かると思います。
そのため、固有振動数を変えるためには、機械の質量を変える、もしくは剛性を変える、という手法が考えられます。
剛性は、断面形状、支持条件、接合条件によって変えることが可能です。
共振によるリスク
機械に共振が発生する場合は、以下のような例が考えられます。
- 高速回転軸で局所的に応力が増大する
- 支持材の柔軟性によって、低周波で共振する
- 長期使用によるネジゆるみや摩耗で固有振動数が変化して共振
これらは、機械を扱っていると、発生し得るものばかりです。
どのようなときに共振が発生するのかを押さえた上で設計することが重要です。
実設計でのポイント
それでは、実際にどのような点が対策ポイントになるのかを説明していきます。
固有振動数をずらす
回転機械の場合に用いられることが多いです。
使用する回転数で共振が起こらないように、質量や剛性を変えて固有振動数を調整します。
減衰を活用する
粘性ダンパーや摩擦を加えることによって、振動を抑制します。
減衰があることによって、共振時の応力を下げることも可能です。
疲労強度を確保する
振動を受け続けることによって、材料が疲労破壊することもあります。
共振だけでなく、疲労強度の観点を持っておくことが重要です。
まとめ
いかがだったでしょうか。
今回は、機械の固有振動数と共振の考え方について解説してきました。
まとめると以下のようになります。
- 機械の振動では、自由度を意識することが重要
- 固有振動数は、質量と剛性によって決めることができる
- 設計時には減衰の活用や疲労強度に注意する
























