皆さんは固体・液体・気体のどれが温度が伝わりやすいと思いますか？
氷のように冷やせる固体でしょうか？水のように冷やせる液体でしょうか？それとも扇風機のように冷やせる気体でしょうか？
今回は温度の伝わりやすさについて解説していきたいと思います。
熱の伝わりやすさの違い
まず、熱伝導における熱の伝わりやすさの違いを考えてみます。
熱伝導は以下の式によって表されます。
$Q=\dfrac{k・A}{d}ΔT$・・・①
$Q$：通過熱量[$W$]
$k$：物体の熱伝導率[$W/m・K$]
$A$：熱が通過する面積[$m^2$]
$d$：熱が通過する距離[$m$]
$ΔT$：物体間の温度差[$K$]
同じ形状で同じ温度差の場合、熱伝導率$k$の値によって通過する熱量$Q$が変わってきます。
式①から考えると、通過する熱量$Q$と熱伝導率$k$は比例関係になっていますので、熱伝導率が大きいほど熱を伝えやすいということが分かります。
同じ熱量で温度を低くできる状態は？
固体・液体・気体の違いを比較する代表例として、氷・水・水蒸気の3つを考えます。
それぞれの熱伝導率は以下の表のようになります。
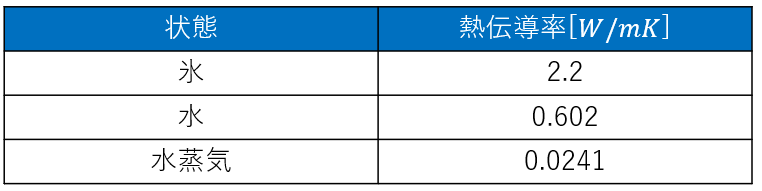
熱伝導率を比較すると、氷が最も大きくなっているため、氷が冷却に向いていることが分かります。
流れがある場合は？
固体が冷却に向いているとはいえ、実際には扇風機や流水で冷やすということも多いかと思います。
液体・気体のような流体の場合は、流れがあるため、放出できる熱量が大きくなります。
流体の流れによって通過できる熱量は以下の式によって表されます。
$Q=h・A・ΔT$・・・②
$Q$：通過熱量[$W$]
$h$：物体の熱伝達率[$W/m^2・K$]
$A$：熱が通過する面積[$m^2$]
$ΔT$：物体間の温度差[$K$]
式①と②から考えると、以下のようになります。
$Q=A・ΔT\dfrac{1}{\dfrac{d}{k}+\dfrac{1}{h}}$・・・③
このように式③の分母に$\dfrac{1}{h}$が入るため、熱伝達率$h$が大きいほど通過熱量も大きくなります。
この熱伝達率は流体の流速が大きいほど大きくなります。
各熱伝達率は以下のようになります。
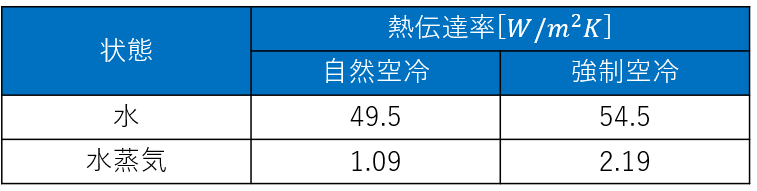
このように強制空冷を与えたとしても、水の方が水蒸気よりも熱伝達率・熱伝導率ともに大きいので、冷却性能は液体＞気体となります。
固体の中に空気が入ると？
実際には固体同士を接触させて熱を逃がすという手法が良く用いられています。
しかし、金属のような固体同士を接触させたとしても、間に空気が入ってしまうので熱が逃げなくなってしまいます。
例えば、伝導する物体の割合を100%固体の状態から、100%気体の状態にするとどうなるでしょうか。
計算した結果を以下のグラフに示します。このとき、熱が移動する距離$d=10mm$として計算しています。
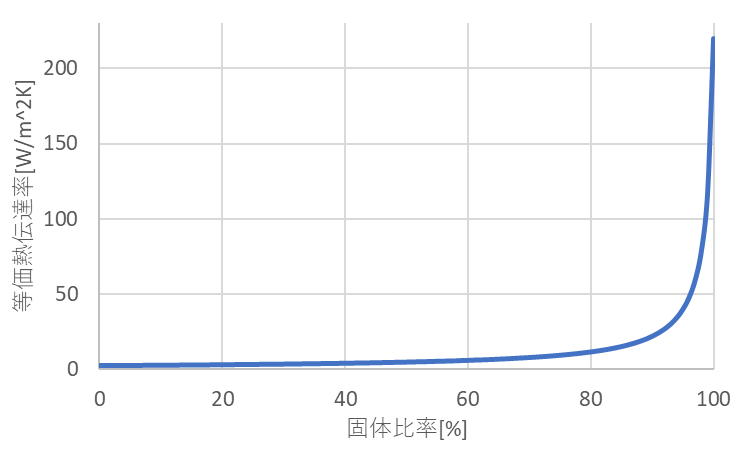
横軸が固体の割合、縦軸が等価熱伝達率を示しています。
この結果から、1%でも気体が入ってしまうと熱伝達する能力は半分程度になってしまいます。
このように熱を逃がさないようにするには、固体間にTIMのような熱を伝えられる物体を挟むようにしましょう。
まとめ
いかがだったでしょうか。
今回は固体・液体・気体の熱の伝わり方について解説してきました。
まとめると以下のようになります。
- 固体が熱伝導率が大きいので最も熱を伝えられる
- 流体の場合は流速が大きいほど熱を伝えやすい
- 固体同士で熱を伝える場合は、間に熱が入らないよう工夫が必要
