回転方向の共振の影響は?【機械力学的解説】

皆さんは回転方向の共振を考えたことはありますか?
本サイト内でも振動に対する共振は何度か扱って、解説してきました。
しかし回転方向の共振はどうでしょうか?
今回は回転方向の共振が発生するときの影響について解説していきたいと思います。
回転軸のモデル
今回は質量$m$の物体を強制振動させる場合を考えてみます。
物体は左右をばねでそれぞれ固定したときの状態とします。
比較のため、2つのばね定数を合計した1個のばねで重心を固定した場合の振動も考えます。
固有角振動数の違い
回転方向を考慮しない場合と考慮する場合の2つに分けて考えてみます。
回転方向を考慮しない場合
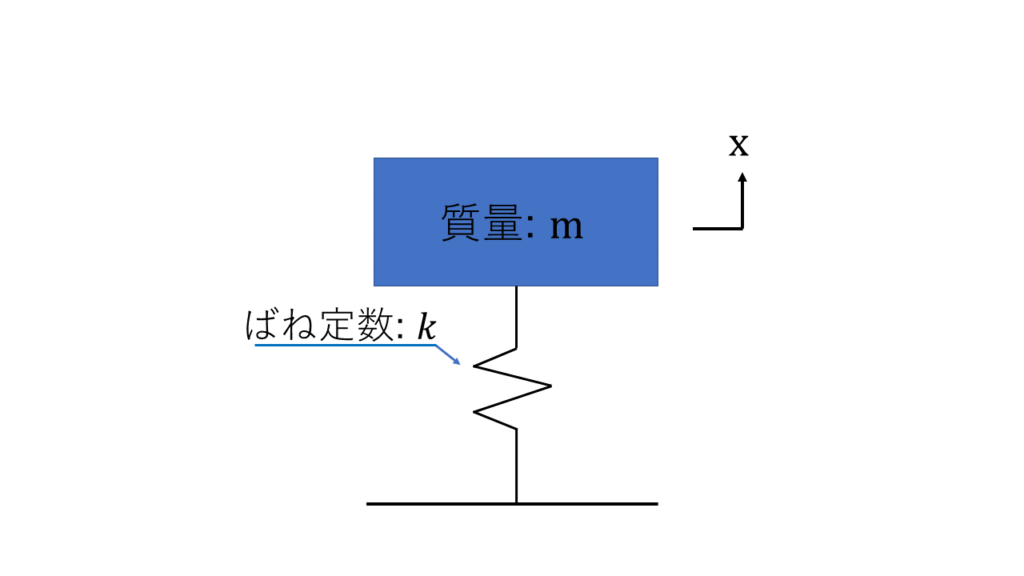
1つのばねによって固定される場合、振動の運動方程式は以下のようになります。
$m\dfrac{d^2x}{dt^2}+kx=0$
$m$:質量[$kg$]
$k$:ばね定数[$N/m$]
このときの固有角振動数は以下のように表されます。
$ω=\sqrt{\dfrac{k}{m}}$
$ω$:固有角振動数[$/s$]
例えば、$m=200kg、k=105kN$とした場合、$ω=22.9/s$となります。
回転方向を考慮する場合
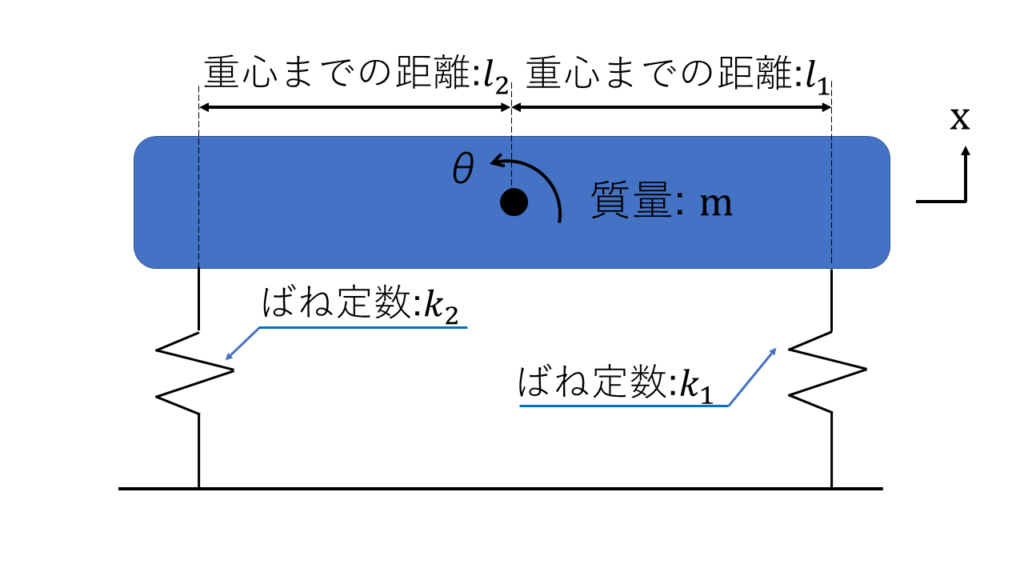
振動の場合の運動を式で表すと以下のようになります。
$m\dfrac{d^2x}{dt^2}+(k_1+k_2)x+(k_1l_1-k_2l_2)θ=0$
$J\dfrac{d^2θ}{dt^2}+(k_1l_1-k_2l_2)x+(k_1l_1^2+k_2l_2^2)θ=0$
$J$:慣性モーメント[$kgm^2$]
$k_1、k_2$:ばね定数[$N/m$]
$l_1、l_2$:重心からばねまでの距離[$m$]
ここで共振する固有角振動数を求めます。
この2つの式を満たす固有角振動数は、以下の式を満たす解になります。
$(k_1+k_2-mω^2)(k_1l_1^2+k_2l_2^2-Jω^2)-(k_1+k_2)^2=0$
この式は$ω$に関する4次方程式なので、実数解は2つ存在します。このように回転方向を考慮することで、共振点が2つに増えるということが分かります。
例えば、$m=200kg、J=40kgm^2、k_1=25kN/m、k2=80kN/m、l_1=2m、l_2=1.2m$とした場合、$ω_1=21.7/s、ω_2=73.7/s$となります。
固有角振動数と質量の関係
ここで質量を変更したときの固有角振動数を考えてみます。他の値は全て前述した値を適用します。
質量と固有角振動数の関係を以下のグラフに示します。
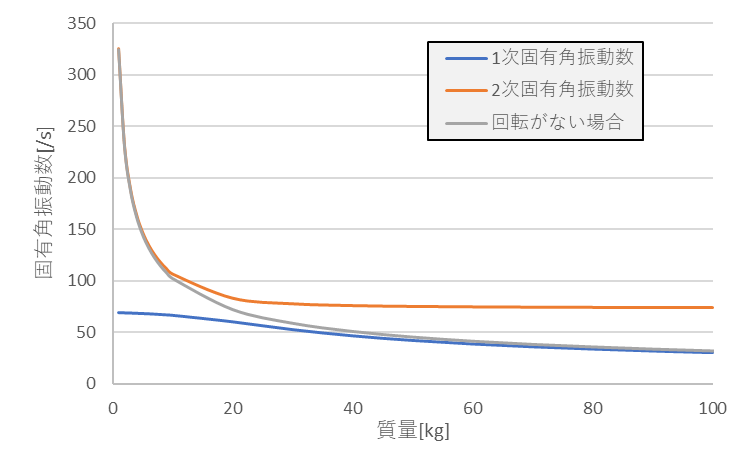
この結果を見てみると、質量を大きくすることで、固有角振動数自体が小さくなっていることも分かります。
つまり固有振動数を小さくしたいは、質量を大きくすることが有効になります。
また、質量を大きくするほど、1次と2次の固有角振動数の差が小さくなることが分かると思います。
1次固有角振動数と2次固有角振動数の関係を変えたい場合も、質量を変えることが有効です。
まとめ
いかがだったでしょうか。
今回は回転方向の共振について解説してきました。
まとめると以下のようになります。
- 回転方向まで考慮すると、共振する振動数が増える
- 質量を大きくすることで、固有角振動数自体を小さくできる
- 質量の値で2つの固有角振動数の差を調整することもできる





















