軸の危険速度の対策法って?【機械力学的解説】

皆さんは回転軸の危険速度という言葉をご存じでしょうか?
回転する機械を設計するときは、必ず意識すると思います。
今回は危険速度と対策方法について解説していきたいと思います。
そもそも危険速度とは?
危険速度とは、回転する機械に発生する現象で、特定の回転数によって軸が共振してしまうことを指します。
この危険速度で回転させてしまうと、回転中の軸の変位が大きくなってしまいます。
つまり想定外の動きになってしまうので、機械自体の破損の恐れがあり、非常に危険な状態になります。
ちなみに共振については、以下の記事で解説しています。
軸の回転数の表し方
回転数の表し方としては、[$rpm$]という単位を用いることが一般的です。
[$rpm$]は1分間あたりに何回転するかを表しています。
また、[$rad/s$]や[$Hz$]と表すこともあります。
この[$rad/s$]は1秒間あたりの角速度を表しており、[$Hz$]は1秒間あたりの振動の回数を表しています。
数式では以下の関係式で表すことができます。
$ω=\dfrac{2π}{60}n$
$f=\dfrac{n}{60}$
$ω$:1秒当たりの角速度[$rad/s$]
$n$:1分あたりの回転数[$rpm$]
$f$:1秒当たりの回転数[$Hz$]
危険速度の起こる原因
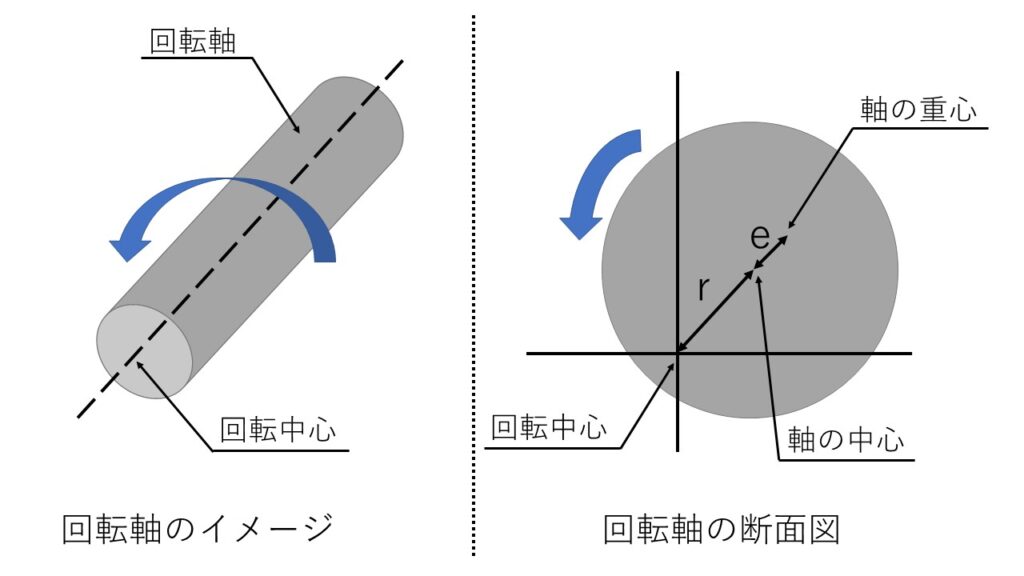
危険速度の起こる原因を数式から考えていきます。
簡単のため、円柱の軸が回転するときを仮定すると、回転時の運動は以下の数式で表されます。
$m(r+e)ω^2=kr$
$m$:軸の質量[$kg$]
$r$:回転軸の中心と軸の中心の距離[$m$]
$e$:軸の偏心量[$m$]
$ω$:回転角速度[$rad/s$]
$k$:回転軸の剛性[$N/m$]
この数式を$r$について解くと以下のようになります。
$r=\dfrac{eω^2}{\dfrac{k}{m}-ω^2}$
この数式の分母が0になったとき、つまり回転角速度と$\sqrt{k/m}$が等しいとき、回転軸の中心と軸の中心の距離が無限に大きくなってしまいます。
これが危険速度が起こる原因です。
例として、$m=1kg$、$k=4N/m$、$e=1m$としたときのグラフを以下に示します。
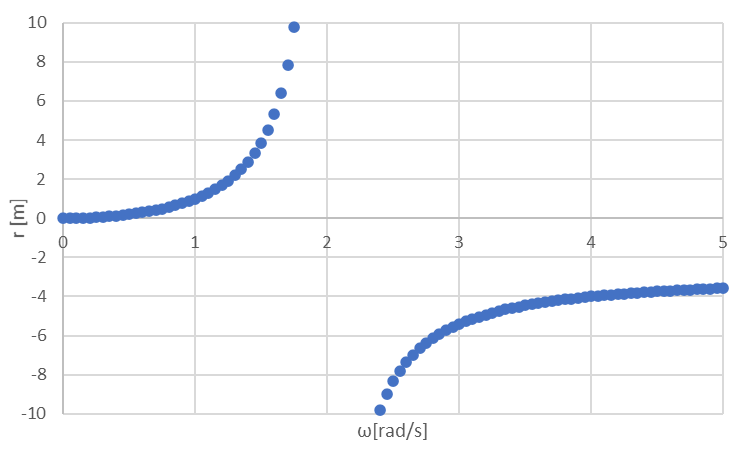
このとき危険速度は$2rad/s$、つまり1分間に約19回転の速度のときに共振を起こします。
危険速度の対策方法
前述の数式から考えると、分子の偏心量$e$を0にすればいいということが分かります。
しかし、実際に物を作る場合、偏心量を0にすると非常に高い加工精度が必要になるので、現実的ではありません。
そのため、先に使用したい角速度を決め、分母の回転軸の質量か剛性を修正することで、危険速度を避けた領域で使用するという方法が用いられています。
具体的には、軸の横振動の振動方程式から、以下のパラメータによって共振角速度を求めることができます。
$ω_n=α_n^2\sqrt{\dfrac{EI}{mL^3}}$
$ω_n$:共振する角速度[$rad/s$]
$α_n$:軸の固定方法によって決まる定数
$E$:ヤング率[$Pa$]
$I$:断面二次モーメント[$m^4$]
$m$:軸の質量[$kg$]
$L$:軸の長さ[$m$]
よって、危険速度の対策をするためには、各パラメータを調整して、使用する回転数から遠ざけることが必要になります。
例えば、共振する角速度を大きくしたい場合、ヤング率$E$か断面二次モーメント$I$を大きくする、軸の質量$m$か軸の長さ$L$を小さくすることが挙げられます。
また、軸を固定する方法が単純支持の場合、固定支持に変更するという方法も考えられます。
まとめ
いかがだったでしょうか。
今回は軸の危険速度について解説してきました。
まとめると以下のようになります。
- 危険速度とは、回転速度によって軸が起こす共振現象
- 危険速度が発生することで、機械の故障などの不具合が生じる
- 軸の固定方法、ヤング率、断面二次モーメント、質量、長さを調整することで、危険速度を調整できる





















